Two Great Developments For Our Electronic Infrastructure

And one of them taught me about something I don't even recall hearing about: orbital angular momentum.

Since I'm wicked excited to dig deep into that, I'll start with the other first.

Sandia National Labs (who inspired me greatly years ago with a picture of their Z-Machine, up top), have created a new heat sink for computers.  Now, I don't know all the ins and outs of cooling computers, but apparently they use both a heat sink and a fan to cool the chips.  This new heat sink is the fan, which is mighty neat.  It is apparently about 30 times more efficient at dissipating heat, drawing air down through the center and shooting it out through the sides, cooling the sink in the process.

This next one uses principles I had never considered, so we're gonna try to go a little in depth on this optical madness.

The Future Is Now

Seems like we've taken all that creativity and ingenuity in virtual worlds and begun applying it out here, via crazy-ass robotics.  Our headspace is leaking into our meatspace, with wonderful consequences.

First, we have the clever idea of bypassing all the difficulty of dealing with terrain by avoiding it completely.  A touch more noble than the tacocopter, I suppose.



The Matternet Vision from matternet on Vimeo

And then we have, as far as I know, the first flying band ever.

No, birds do NOT count.

Oh, Be A Fine Girl...

One of the nice things about stars is that they are, in their own way, fairly simple things.  Just a bunch of Hydrogen, some Helium, trace amounts of other elements, mushed together by gravity so powerfully that they ignited.  Their general behavior is almost entire defined by the amount and proportion of their chemical makeup.  And there's so very many stars knockin' about, we've cataloged enough to present a decent continuum of possible states.

(23,000 stars plotted on an HR Diagram)

Another nice thing about stars is that we can basically see their insides, via the electromagnetic energy pouring out of the surface.  This energy is characteristic of the reactions taking place.  Spectroscopy studies this relationship between matter and photons.

There are three ways matter emits light that are of interest to scientists.  One is the common black body radiation, based on the temperature of very hot things (when you see heated objects turn red, this is black body radiation).  Because they're all jostling about, it forms a continuous spectrum.  The second is emission spectra, which peak at wavelengths characteristic of the chemical reactions/electron excitations/ionizations.  The third, the converse of emission, is absorption.  When a continuous spectrum of light falls on some cool and mostly transparent gas, the gas can absorb specific wavelengths of light, leaving a vacancy in the continuity.  Thus, the emission spectrum of a material has bright lines in the same place that it's absorption spectrum (with a continuous background) would have dark lines.

These are actually known as Kirchhoff's laws:

1. An incandescent solid, liquid, or gas under high pressure emits a continuous spectrum.
2. A hot gas under low pressure emits a "bright-line" or emission-line spectrum.
3. A continuous spectrum source viewed through a cool, low-density gas produces an absorption-line spectrum.

Spectroscopy is the analysis of these laws; the light is sent through a diffraction grating, spreading it's differing wavelengths.  Spectral analysis was already happening with materials on Earth for a few decades, but in the late 1800's Kirchhoff had the clever idea of aiming that analysis upwards.  For the first time humanity knew that the objects up there were made of the same material as objects down here.  As a quick example lets look at Helium, which was actually discovered in our sun 14 years before it was discovered on Earth, even deriving its name from Helios, Greek mythology's personification of the sun.

Helium Spectrum

Hydrogen Spectrum

Now, with quantum mechanics, we can understand the existence of these characteristic lines in terms of an electron raising or lowering its energy state.  

So using spectroscopy, we can understand the composition of a star.  We can know the temperature, by its black body radiation, and we know how much energy it takes to, say, ionize Hydrogen, so we know what's going on if we see that spectral line.  Looking back up top, you can see how the cooler stars (O, B, A...) have two Hydrogen absorption lines (corresponding to the Balmer series), which imply that Hydrogen in its second excited state is absorbing photons.  The hotter stars indicate the existence of Helium with it's characteristic yellow line.  And this is all just along the range we're lucky enough to spot with our eyes.  This analysis can take place across the entire electromagnetic spectrum.

It's almost too mad to consider: we can determine the chemical make-up of things we'll never go near, just by the information it beams outward - a story told in all directions of it's internal structure, so long as you're (scientifically) literate enough to read it.

Link: Dynamics of Political Ideologies

One of the major insights from works such as The Origin and Evolution of Cultures is that human societies can adapt and map themselves upon the environment with a few simple heuristics. A primary dynamic by which group behaviors propagate and enforce themselves is the do-what-my-neighbor-does rule-of-thumb. Obviously this is not always optimal. Sometimes it is needful to think for oneself. But thinking for oneself is cognitively expensive. Doing what everyone else does is cheap. Figuring out what you want to do for yourself is time consuming, and requires deliberation. There are analogies here between “hard & fast” reflexive cognition, and “slow & deliberate” reflective cognition.

Reading is good for you. 

Diffraction In Your Camera (And Everywhere Else)

In the 'Oh, is that what that is?' category...

Diffraction, in the simplest description, is what happens when waves encounter objects.  Their patterns tend to bend and distort, such as up top there, where plane waves become spherical waves by passing through a slit.

Light, as you might guess, experiences diffraction as well.  Here's a schematic of light passing a sphere.

Irrelevant to today's topic, but those 'lines' extending to the right from the sphere are interference patterns.  Where they are exceptionally bright, it is constructive interference, and the received light would actually be brighter than the original beam.  The dark parts are destructive, and can actually result in no light being received.

And one day, when you're older, I'll tell you all about phase differences and explain that whole shebang.

But today isn't about that.  Today is about a very familiar phenomenon to pretty much everyone: diffraction spikes.  Take it away, NGC 6397!

Yeah, those things.  Perhaps you'd like something more familiar, and we can accommodate.

You may have put two and two together by now.  If you're gonna take a picture, you'll most likely need some lenses, maybe even a mirror.  These items need to be held in place, with clips or rods or what-have-yeh.  When the light hits these holders, it bends around them, distorting into these spikes once they get to the film/receiver.

One neat thing is that you can use these pictures to tell you how many holders, and the orientation of them.

Not everybody appreciates these spikes, so sometimes a person will close the aperture to exclude the outer circle, in some cases people even go so far as to manually remove the front part of a clip (if they had, for instance, a telescope they never intend on tipping forward).

Interesting to note: diffraction is dependent on the wavelength of the light, so that different colors of light will diffract at different angles.  If you look back up at the nebula picture, you see an alternating blueish/reddish pattern.  The interference pattern's intensity(number of photons) looks like this:

So that when you have a longer or shorter wavelength, the peaks shift outward or inward, respectively.  If you do this with white light through a diffraction grating (a small sheet of material with hundreds or thousands of tiny slits to see through), you get a truly gorgeous result of light's wavelike behavior.

(That's a single wavelength on the top, with a full spectrum on the bottom)

You can see how the red light, with its longer wavelength, spreads out further and faster than the higher-energy, shorter-wavelength blue light.

Since I'm on the subject here, take an opportunity right now to curl up your forefinger so that only a little bit of light can get through it.  Aim it between your eye and some white part of this screen, and adjust your 'aperture' as you peer through.  You will notice little dark lines and dots showing up in the middle where nothing is touching.  Those are spots of destructive interference, caused by your own hand!

And this is why it used to be so much easier to discover new laws of physics in your own basement.

Random vs. Non-Random Fractals

"Clouds are not spheres, mountains are not cones, coastlines are not circles, bark is not smooth, nor does lightning travel in a straight line." - Benoit Mandelbrot 

On occasion, I notice some confusion about fractals.  Namely, about the difference between the idealized ones we create like the Sierpinski Gasket or Mandelbrot set, and the ones we see in nature, like trees/deltas/grass/lungs/nerves...well, all kinds of things, really.  Folks will sometimes take one idea from non-random fractals - that they show self-similarity across all scales, forever - and combine it with two perspectives on the physical world - that the deeper we probe, the more we find, and that sometimes across some scales we find fractals.

Take that figure up top - the Sierpinski Gasket.  Take a shape, like a triangle (Fun Fact: it doesn't have to start as a triangle, all shapes approach the same final behavior).  Get three of those bad boys together and stack them as seen in the second figure.  Take that shape and two of its friends, stack them similarly.  Repeat for like, ever.

This is a nice, non-random, utterly unnatural, geometric fractal.

There are other ways to build fractals.  The Mandelbrot set is a map of initial conditions.  Basically, given some iterative sequence such as the one above, how does it end, given some initial value?  Some visual aid for you:

So, if the iteration grows infinitely, it is not considered part of the set.  If it dies down, or stays in some stable range, it is.  Thus the black areas up there are all numbers which, when plugged into the iteration, result in some finite value.  What you see is a map of initial conditions.

And as I'm sure you've held witness to before (one example of many), you can see how the entire shape is repeated on smaller scales, infinitely.  Which is not to say it is infinitely complex.  It is actually very simple, it just gives rise to a shape we have difficulty describing with our familiar geometries and intuition.

With me?  Good.

Lets move on to random fractals.  Naturally occurring self-similar patterns with boundaries.  From From Newton To MandelBrot by Stauffer and Stanley:

...no non-random fractals are found in Nature.  What is found are objects which themselves are not fractals but which have the remarkable feature that if we form a statistical average of some property such as the density, we find a quantity that decreases linearly with length scale when plotted on double logarithmic paper.  Such objects are termed random fractals...

The difference is that in the real world, patterns are made of things.  They are not perfect mathematical objects without limitations.  Fractal geometry will help you map a coastline, but zoom in far enough, and you find particles with no interest in deforming themselves to fit your notions.  Ferns make for distinct fractal patterns within a few scales; a group of leaves made of smaller, similar groups of leaves, looking not entirely unlike the leaves themselves.

But notice, that's where the scaling, the self-similarity, ends.  The cells don't look like the leaves, and I imagine a forest of ferns wouldn't look much like a fern either.

So these natural fractals only exist within certain bounds.

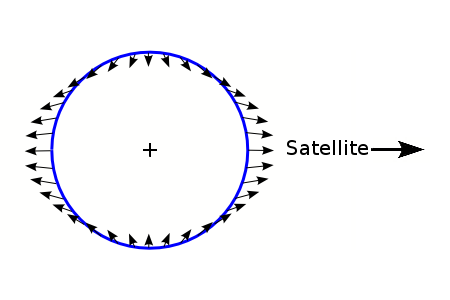
Say, while we're here, if you don't mind terribly, I'd like to put to rest a little notion that comes up here and there: The orbits of electrons and the orbits of planets are unequivocally not similar in any respect.  One is held in place by its own momentum and the gravitational pull of the sun, while the other is held into place by strict and peculiar quantum mechanics and electromagnetic forces.  Unless you can find us some planetary orbits that look like these...

Ok!  Thanks for allowing me that.

So like I was saying, natural fractals don't exist on all scales, for various reasons.  The universe is a very busy place, and just when you think a pattern may begin emerging, some parameter, some interference somewhere, tends to put a stop to it.  Gravity is trivial at small sizes, get too big and you might crush yourself.  A sand dune can never get as small as the grains that compose it.

The universe is a brilliant zoo of patterns.  Geometric, fractal, exponential,  periodic, chaotic (that is, utterly non-patterned).  The rules governing scaling behavior, networked interactions, are used in research across the academic spectrum - chemists depositing chemicals onto substrates see them, botanists modeling plant growth use them, neurologists trying to understand the distinctly non-linear computing power of the brain are forced to address them.

But the universe itself is all those things and so much more.


I hope I get to share more of it with you.

What This Blog Is Really All About

The (Not) Faster-Than-Light Neutrinos

Hey, y'all remember when neutrinos exceeded the speed of light?  Sure ya do!  Scientists were befuddled, pseudo-scientists came out of the woodwork yelling 'SEE!?  SEEEEE!?' as they like to do.  Einstein was wrong, physics has to be rewritten, all that sensational nonsense.

So,short version: they didn't.

To recap, last year CERN produced some delightfully titillating results when they produced some neutrinos in an accelerator, and then shot them in the general direction of Geneva, some 450 miles away.  One of the nice things, as you may recall from your favorite blog ever, about neutrinos is that their lack of electromagnetic interaction can send them through the Earth with little to no interaction with the planet itself, making it a primo substance for shooting directly from one city to another (and inducing a fevered pipe dream of using them for communications...).  They made a most peculiar discovery: the neutrinos arrived about 60 nanoseconds quicker than the speed of light allows!

Now, these were fairly preliminary results, but the scientists at CERN had difficulty figuring out what could have been going wrong.  For instance, the beams of neutrinos they were sending were potentially long enough to cause confusion (are we detecting the front exactly, or somewhere else?).  Detection issues, departure and arrival issues, miscalculations; as exciting as it would be to deny a fundamental aspect of our physical model, what it really does to scientists is freak them the hell out. 

One of the main points of contention involved the Supernova 1987A, discovered in...1987.  A few hours before the visible light reached us, before we had any idea it was going on, three detectors around the world had an extremely active burst of detection; that is, a total of 24 between them in a 13 second period (remember, they usually only detect 1 or less per day).

Now, the light that arrived had to interact with all that interstellar matter, so it was slowed substantially.  The end result, however, was that neutrinos traveled ever-so-slightly slower than the speed of light.  And one would rightfully suspect that if neutrinos actually did travel FTL, it would become obvious over the 168,000 light years it traveled to get here.

A few months after these preliminary superluminality (Word of the Day) results, two problems emerged in their analysis; a malfunctioning clock, and a "leaky" fiber-optic cable.  Correcting for those, now the final results are in, presented at the annual neutrino conference: the neutrinos made the 450 mile trip 1.6 nanoseconds after the speed of light would allow.

The universe's top speed holds steady, humanity makes some of the most accurate measurements in species history, and the world learns a lesson about preliminary findings.

Just kidding about that last one.  We'll never stop being goofy.

Lunar Tidal Forces and the LHC

Hey errybody!  How've you been?  Good, good.

Did you know the Moon is squeezing the Earth?  It is indeedy.  The Earth's generally pretty solid, so it can be hard to notice.  Water however, is not quite so solid.  Lucky us!  The world would surely be less interesting without tides.

Up there is a schematic of the effects of a strong central gravitational force some distance away.  For us, it causes tides, mostly due to the Moon, with about half as strong of an effect from the Sun.  Heck, its even doing it to your mushy, watery body, just not with any strength we're capable of detecting (nor are we wide enough). (Fun Fact: these are the same forces that cause the popular "spaghettification effect" when falling into a black hole)

So what?  Sew buttons!  Because something like the LHC, about 3 miles wide, is indeed big enough to feel these effects.  I'll let the shift leader at the time explain:

Data was coming in at a high rate and all sub-detectors were humming nicely. Not a glitch in hours so we were getting slightly sleepy nearing the end of the shift around 22:00. So when a colleague from the trigger system (the system that decides which events are worth keeping) called to inquire about recurrent splashes of data, I was rather puzzled.

I quickly went around, asking a few shifters to check their system. Nobody had a clue. Then I took a closer look at this plot that I had not scrutinized before since everything was so seamless.

What she was perturbed by were those dips in the lower two curves, which measure the intensity of the collisions.

So I called the LHC control room to find out what was happening. “Oh, those dips?”, casually answered the operator on shift. “That’s because the moon is nearly full and I periodically have to adjust the proton beam orbits.”

This effect has been known since the LEP days, the Large Electron Positron collider, the LHC predecessor. The LHC reuses the same circular tunnel as LEP. Twenty some years ago, it then came as a surprise that, given the 27 km circumference of the accelerator, the gravitational force exerted by the moon on one side is not the same as the one felt at the opposite side, creating a small distortion of the tunnel. Since the moon’s effect is very small, only large bodies like oceans feel its effect in the form of tides. But the LHC is such a sensitive apparatus, it can detect the minute deformations created by the small differences in the gravitational force across its diameter. The effect is of course largest when the moon is full.

Humans are amazing.

Enjoy your weekend!

When Galaxies Collide, Solar Systems Survive

You may have caught this making the rounds as of late: Astronomers Predict Titanic Collision.

It's been known for some time that Andromeda and the Milky Way are moving towards each other, and the end result somewhere down the line would be a very large elliptical galaxy (Fun Fact: galactic collisions always end in elliptical galaxies, meaning that spirals are slowly dying out).  It was possible that the galaxies would whip  and distort and orbit around each other for a rotation or two before eventually settling down as one.  It's the kind of thing that takes hundreds of millions of years, but still happens...well, fairly often actually.

(More hot, gassy, galaxy-on-galaxy action here)

So the news here is that we've done some very, very precise calculations.  It's actually quite hard to tell how fast and in what direction celestial objects are heading.  The results?  We are heading right for each other.  Collision in T minus four billion years.

Oh my yes.

There is good news!  The good news is that by then, the oceans will have evaporated, the atmosphere would have been blown off, and life on Earth probably wouldn't exist anymore.

Wait, no, that's not the good news.  Dammit.  Ah, here it is: yes, the good news is that while we are speaking of galaxies 'colliding', it is very unlikely that actual solar systems would do anything of the sort.

Galaxies, despite their appearance, are mostly empty space.  Really empty.  Consider, the nearest star to us is about 4 light years away.  The average density of stars in our galactic neighborhood is about a star per cubic light year (our solar system is about 0.0006 light years wide).  This means that, while our solar system's position relative to other stars may be distorted, even our planetary orbits have little chance of being directly effected.

There is a lot of gas around, however.  And when you get one galaxy rubbing against another galaxy, their gaseous forms getting all hot and excited when they join together, as chaotic and blind as any prom night, you get...well, what do you think you get?

You get babies.  Collisions like this are a prime generator of stars.

See?  LOTS of good news!

Video: A Bit of Chaos

Here's a quickie, showing some of the basics of nonlinear dynamics, which I think is one of the most interesting fields in physics.  You've probably heard of an aspect of it, sensationally named chaos theory.

(Image Credit: Bugman123: http://www.bugman123.com/Fractals/index.html)




A good deal of nonlinear systems arise as a combination of forcing terms and dissipation terms.  Say, for instance, you throw a handful of feathers - there is the initial force of the momentum you give them in the throw, and the force of gravity pulling them downwards.  And in a place with no atmosphere, it would be a very simple bit of behavior.  But with air, a dissipation term comes into play, sapping the momentum and impeding the gravity.

Or, say, you had a pendulum, released from some height (forcing), above some magnets (dissipation).

Sensitivity to initial conditions really means sensitive.

If you notice towards the end of the clip there, you'll see what amounts to random fuzz in the map.  This, specifically, is where the chaos is.  Much like the shaded part in this bifurcation diagram (think of the x-axis as the distance the pendulum is pulled from the center).