Possible Dark Matter Detected

Dark matter, as you might gather from the name, is impossible to "see" (in the sense of reflecting light).  Whatever it may be specifically, it most certainly doesn't seem to interact electromagnetically with any other particles.  And so we turn to other forces to detect it - most notably gravity.  It's existence was first inferred from the inexplicably high gravitational energy necessary for the observed speeds of galactic rotations (and the speeds of galaxies in clusters).

"Hang on, Doc.  I see something that makes no sense."

The Magic of Gyroscopes

"Somebody for the love of god explain to me how that works, how the fuck does that happen?"
 - Bill Burr

Sure!  I heard Bill bring this up on the Joe Rogan podcast, and since my intended next post is becoming more long winded than I hoped, I thought this would make for a nice subject.

Let's start with Newton's first law: objects in motion tend to stay in motion, and objects at rest tend to stay at rest, unless acted upon by some outside force (force is an important word here).  This concept is at the core of inertia, the resistance an object has to change in it's behavior.  There is a basic kind of inertia in reference to motion, with mass being the basic measure of an object's resistance.  But there is also a rotational inertia, based on both the mass and the shape of the object, along with defining exactly which axis you are rotating the object around.

Once you start an object a'spinning, the combination of the angular speed and the rotational inertia defines the angular momentum.  In the case of a wheel-shaped object spinning as the one in the video, this momentum can be imagined as an arrow pointing out from the axle (I know it's odd to imagine that the angular momentum is directed perpendicular to the actual rotation, but just trust me that it works out mathematically).

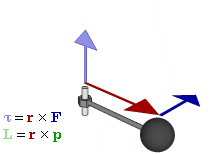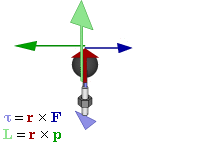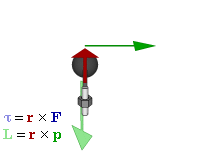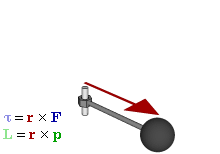L is the angular momentum.  Torque (T) is the applied force.
(wiki)

So now we've got that arrow sticking out the side.  Imagine two more arrows: one pointing upward, which is the force of the rope holding the wheel up.  The other is downward, due to gravity pulling it downward (and it is in fact a torque, as 'falling' would cause the object to rotate around the point where the rope holds it up).

By Newton's law, we know that this angular momentum, pointing outward, will resist any disturbances in it's speed or direction.  And thus, so long as it is spinning fast enough (increasing the value of L), the wheel resists being pulled downward by gravity - indeed, tries to resist tilt of any kind.  That outward arrow remains as constant as possible.  This is exactly why it's easier to maintain balance on a bike when you're moving faster - below a certain speed, the angular momentum is overwhelmed by the forces of gravity.  Likewise, a top, or that wheel above, as they slowed, would begin to fall as their resistance to a downward pull weakens.

You see that r in the above equations?
That stands for radius, and a larger radius makes for a larger momentum/torque.
And that's why those goofy Victorian bastards thought a giant wheel was a good idea.

As gravity is a force, it is being applied perpetually, pulling and pulling ever downward.  So, if you imagine the upward (rope) arrow staying constant, and the outward arrow of momentum trying to stay constant, the ever-pulling grip of gravity must somehow be answered, which the wheel does by slowly twirling around the rope, in a horizontal redirection of the downward force.

Hope that wasn't too difficult of a read.  To technically understand the rotation of three dimensional bodies is surprisingly unintuitive.

"Science is like, it's incredible, isn't it?"
 - Bill

Fermions and Bosons

Welcome back and hello new friends!  Let's ignore the lengthy gap between this post and the previous one and hop right on it, shall we?

The Higgs boson inferred from LHC experiments has been in the science news often lately - most recently they're now super-duper sure it's a Higgs, which is thrilling in that "oh snap, we were right" kind of way.  And whenever you hear an explanation of what the Higgs is or does, you never really need to understand the boson to follow what they're saying.

So, what is a boson?  This comes with a free complimentary question: what is a fermion?  We start with the characteristic difference between them: spin.

On your first consideration, you may be insulted that someone would suggest you don't know what spin means.  In all likelihood, if you're reading this, you have a computer chair.  Ipso facto, you know what it means to spin.

Go ahead, take a few spins right now.  I'll wait.

But there's some qualities of this kind of spin that you take for granted: you have a size, and you're not rotationally symmetric.  Electrons, for instance, do not have this luxury.  What you think of as spinning is generally an orbital angular momentum - parts of you are orbiting around a central axis, that is, travelling in a circle.  To oversimplify, the magnitude (strength) of this spin is defined by the speed the part is moving, multiplied by the distance of that part from the axis.  This is the physics behind why doorknobs are as far from the axis of the door's rotation as possible: this larger distance minimizes the effort needed to actually open it.

So, how do you describe spin for an elementary particle with effectively no size, and no way to tell the back from the front?  The 'distance' from the axis goes to zero, implying the orbit is also zero.

Classically, the proposition makes no sense.  And yet in 1922, Stern and Gerlach were forced to suggest that these structureless particles nonetheless possessed an intrinsic angular momentum.

From Quantum Physics by Zettili (easily my favorite textbook on the subject, dense and complete):

In the Stern-Gerlach experiment, a beam of silver atoms passes through an inhomogeneous (nonuniform) magnetic field...we would expect classically to see on the screen a continuous band that is symmetric about the undeflected direction...According to Schrodinger's wave theory, however, if the atoms had an orbital angular momentum l, we would expect the beam to split into an odd (discrete) number of 2l+1 components.  Experimentally, however, the beam behaves according to the predictions of neither classical physics nor Schrodinger's wave theory.  Instead, it splits into two distinct components...

(Sauce: wiki)

This experimental result only made sense when one suggests that the particle carries an inherent angular momentum.  Not only that, but this spin comes in discrete values.  Imagine if you could only spin in your chair at specific speeds (lost in thought, too fast, and nauseating).  And then forget that image, because you weren't actually spinning in any spatial direction, you merely contain "spin".  Ridiculous, I know.  As Zettili puts it, "The spin, an intrinsic degree of freedom, is a purely quantum mechanical concept with no classical analog".

As stated, spin comes in discrete values; specifically it comes in half-integer values - 0, 1/2, 1, 3/2, 2 (all multiplied by Planck's constant, as so many quantum characteristics are), and so on.  Finally we approach the issue brought up at the beginning of this post: spin is the defining characteristics of bosons and fermions.

Bosons have "integral" spin; 0, 1, 2, etc.  This class of particles most importantly contains the photon (and of course, the Higgs).

Fermions have spins like 1/2, 3/2, 5/2, etc, named "half-odd-integral spin" (because even halves like 2/2 is just 1).  The most significant fermion is the electron, but also includes protons, neutrons and quarks.

So what's the importance of making this distinction?

(a) Asymmetric and...

(b) ...symmetric wave functions (wiki)

Without getting into the details, having a half-odd or integer spin defines how you interact with other, identical particles.  You can define a group of identical particles by a wave function, and a group of fermions (half-odd spin) has a wave function which is described as asymmetric (Figure a above), while a group of bosons would be described by a symmetric wave (b above).

In the symmetric case, nothing particularly interesting occurs; you can effectively stuff as many bosons as you want into one space, and the wave function accommodates them quite pleasantly, not unlike being able to add as many musical notes to a chord as you like.  The wave abides.

"That Higgs is really keeping this room together."

However, in the asymmetric case, the wave function describing the state of multiple identical particles does a funny thing; if you pretend to put two fermions in the same state, the value of the wave function goes to zero. That is, such a wave function doesn't exist, can't exist, under the constraints of quantum mechanics.  This results in the popular Pauli exclusion principle; try as you like, you simply can't stuff as many electrons as you like into one state: this exclusion repels the electrons away from each other, quite strongly.  This "degeneracy" (multiple particles occupying the same energy level) is responsible for the relative "imperviousness of solid matter" in the case of electrons, and what keeps neutron stars from collapsing (as fermions, neutrons also are constrained by exclusion).

This principle is also the reason for electrons taking positions of increasing energy states in atoms.  In fact, it is at the core of all atomic and chemical interactions.  It defines much of the character of the periodic table as well.  The rows are made by increasing the number of electrons within a "shell", with each subsequent row representing a larger shell, and each column representing similar "filling" of each shell.  In fact, without this exclusion (that is, if electrons were bosons), the universe would be a very dull place indeed, as all the electrons of an atom would fall to the ground state, and all atoms would behave the same.

This all tells you pretty much nothing about the Higgs, but I hope it illuminates just a little bit more of the universe.

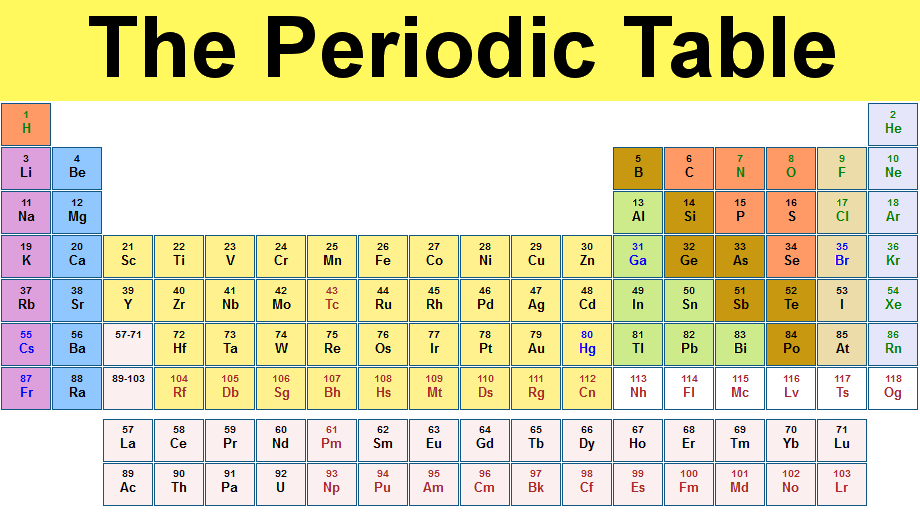(sauce: chemicool.com)

Tidal Friction

Just put that on while you read this.  I'm serious.  Turn your nonsense off.  That is sexy music.

Nay.  It is sex music.

So, (he said, as though there were no such thing as a long absence), I was thumbing through this month's Discover, reading an interesting article on the possibility of life on other celestial objects in our solar system ("Frozen. Irradiated.  Desolate.  Alive?"), and came across this statement:

Although located a half-billion miles away from the sun, [Europa] receives a strong tug from the gravity of mighty Jupiter that warms the moon's insides.

 BRILLIANT!

Tidal forces, as readers very well know, can have significant effects on large things.  But here on Earth, tidal forces are rather simple.  Our moon has already settled into a synchronous rotation, always showing the same face.  Like this!

(wiki)

(Fun Fact: this gif is apparently going to play the entire time I type this.  Blogger is weird.)

I say the moon 'settled' into that rotation, and I really do mean it.  Nature, when unperturbed, tends to reach for the lowest potential energy needed to continue doing whatever it's doing.  Back when the moon spun relative to Earth, there were indeed friction: imagine a point on the surface of a spinning moon, tracing out a spirograph-like pattern in it's orbit around the Earth.  As that point draws away from the planet, it is fighting against a gravitational pull, that it's corresponding point on the opposite doesn't suffer: it's motion towards the Earth is actually strengthened.  This asymmetry contributes to frictional forces that, over time, serve to slow the rotation of the moon (and indeed, to a slight extent, the Earth).

Friction is an agent of entropy - mathematically, you can consider it a dissipation term (in a different context, mentioned here), it makes for a more even distribution of energy, the result in this case being an 'easier' (lower energy) orbit.

But I digress.

The article was talking specifically of this tidal heating happening in Europa (Jupiter's second moon), but the most significant object in the solar system subject to this is Io, Jupiter's first moon.

As I have literally just now learned, Io is in a resonant orbital period with Europa and Jupiter's third moon, Ganymede.

Fun Fact: their resonance prevent a triple conjunction (all three moons aligning on the same side) from ever happening.

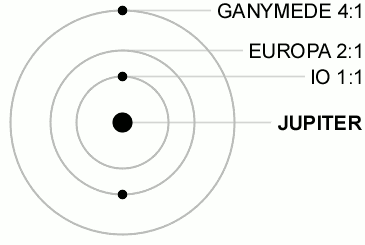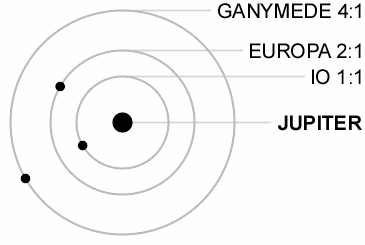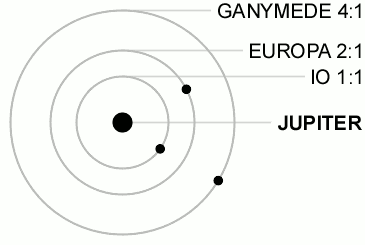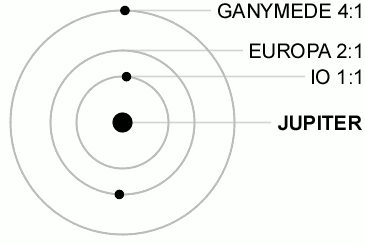(wiki)

Unlike the moon, Io has to deal, every other 'year' (it actually does a full orbit in 1.8 days!), with a secondary moon yanking and tearing at it from the other side of Jupiter's (much more significant than Earth's) gravitational pull.  Even the pull of Ganymede and the fourth moon Callisto contribute to this internal turmoil.  Io is tugged and torn, squeezed and stretched, from seemingly every side, in perpetuity, in every orbit, resulting in it being named the most "geologically active" object in the solar system, with over 400 volcanoes.

You are beautiful, Io.  No matter what they say.

This all speaks to the odd combination of weakness and power in gravity: it is, by distance, the weakest of the forces (strong, weak, electromagnetic), and yet it attracts everywhere: galaxies across the universe tug imperceptibly, inconsequentially, on our home, our bodies, our fingers.  When we do see the interesting and complex behaviors that can be caused gravity, it is in the great masses of planets and moon - themselves so massive they have crushed themselves into spherical objects.  And surely, there are even more peculiar behaviors out there, cause by the gentle ever present tug of gravity.

Oh, and if you wanna learn about why it's so important on Europa, you'll have to read that article too.  GOTCHA!

Pictures of Molecular Bonds

Photography!  You know a little bit about it, right?  You get a film or screen or some such, let some photons hit it for a while, and voila, you got yourself an image.

but you know about photons too.  You know that if something is small enough, the momentum of photons is likely to knock them about.  You may even know that the resolution is restrained by the wavelength of the photon - the longer the wavelength, the less their resolving power.  Think of it like pixels - the larger the pixels, the worse the image.  So how do you take a photo of something very, very tiny?  You use something with a shorter wavelength, of course.

Like electrons!  See, you could use visible light, around 400-700nm (billionths of a meter) to see...well, all the things you see, or X-Rays, at 0.01-1nm to go through tissue and bounce off denser material such as bone.  But these are still general surfaces, much too blunt for our purposes.

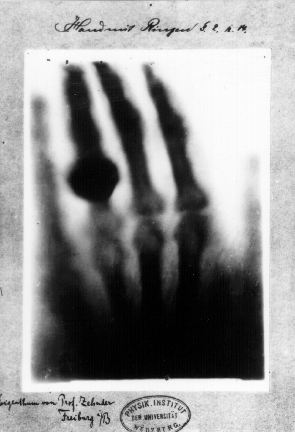First "medical" X-Ray image: Roentgen's WIFE'S hand.
Not what I would call chivalrous. (wiki)

Gravity's Effect On Perception

You may have, at some point in your life, noticed gravity.  Good!  It's super-important.

Gravity has been with us for our entire biological evolution.  Thus it only stands to reason that our biology would, when possible, take advantage of its influence.  For instance, since gravity on Earth is always pointing downward (technically inward, as a central force), it makes for an extremely reliable vertical compass.

FUN FACT:  the strength (and indeed, even direction) of gravity on the Earth's surface actually varies from location to location, dependent on factors like altitude, the local topography (say you had some mountains nearby) and geology (distribution of density).

Sauce

Local gravity can even change over time, due to differences in water levels and such.  Here's the gravity in South America shifting as the floods and recedes (holy snickerdoodles we're smart enough to watch gravity change from space):

Oh right I was going somewhere with this.

So, important and unavoidable as it is, gravity has been a perpetual influence in our evolution.  How else would you walk and balance yourself, how else would you know the orientation of your head, if not for an ever-present acceleration?

It also makes sense that gravity's influence would have seeped into other aspects of our brain.  Here we get to the whole point of this post: scientists conducted some visual illusion experiments on astronauts before, during and after trips into space, and found an interesting trend concerning vertical perception of these illusions.

Here's the Inverted-T illusion (wherein each line is actually the same length), with a graph detailing the perceived size difference by participants at various times:

They also asked participants to draw squares and crosses, measuring the horizontal-to-vertical ratio.

The extremely wide error bars are due to the small sample size, but the trend exists nonetheless.  As they spend time in space, a seemingly gravity-induced perception of vertical length dissipates.

One of the primary causes of speciation (if not the primary cause) in biology is some sort of geographic or geologic separation.  I can think of no geographic separation more significant than departing the planet altogether.  As people take longer and longer trips (longest cumulative time belonging to Sergei Krikalev with 803 days), it will be interesting to see the effects on human physiology and psychology, and how that will confer benefits and differences.  Sure, bone and muscle density decreases, but who needs bones in space?

h/t Neuroskeptic (amidoingitrite?)

Wicked Coronal Mass Ejection

So there was a gigantic explosion on the Sun the other day:

First of all: good gravy that is beautiful.

These cooled filaments (this one half a million miles long) are masses of charged particles held in place by the Sun's magnetic field.  The Coronal Mass Ejection you see takes about an hour, and is traveling at 900 meters per second (about 2000 miles per hour).

Here's pictures at four different wavelengths (all in the X-Ray spectrum):

The variety of wavelengths helps scientists watch the change and distribution of temperature.

Even though it was directed away from us, the blast expands spherically, so we did catch some of the ejection about four days later, resulting in even more beauty, as charged particles smash into the Earth's atmosphere and emit Bremsstrahlung ('braking') radiation:

It's enough to make you think there might be something slightly dangerous about a slow, fiery nuclear explosion the size of 100,000 Earths.

http://www.nasa.gov/mission_pages/sunearth/news/News090412-filament.html