Welcome back and hello new friends! Let's ignore the lengthy gap between this post and the previous one and hop right on it, shall we?
The Higgs boson inferred from LHC experiments has been in the science news often lately - most recently they're
now super-duper sure it's a Higgs, which is thrilling in that "oh snap, we were right" kind of way. And whenever you hear an explanation of what the Higgs is or does, you never really need to understand the
boson to follow what they're saying.
So, what is a boson? This comes with a free complimentary question: what is a fermion? We start with the characteristic difference between them: spin.
On your first consideration, you may be insulted that someone would suggest you don't know what spin means. In all likelihood, if you're reading this, you have a computer chair.
Ipso facto, you know what it means to spin.
 |
| Go ahead, take a few spins right now. I'll wait. |
But there's some qualities of this kind of spin that you take for granted: you have a size, and you're not rotationally symmetric. Electrons, for instance, do not have this luxury. What you think of as spinning is generally an
orbital angular momentum - parts of you are orbiting around a central axis, that is, travelling in a circle. To oversimplify, the magnitude (strength) of this spin is defined by the speed the part is moving, multiplied by the distance of that part from the axis. This is the physics behind why doorknobs are as far from the axis of the door's rotation as possible: this larger distance minimizes the effort needed to actually open it.
So, how do you describe spin for an elementary particle with effectively no size, and no way to tell the back from the front? The 'distance' from the axis goes to zero, implying the orbit is also zero.
Classically, the proposition makes no sense. And yet in 1922, Stern and Gerlach were forced to suggest that these structureless particles nonetheless possessed an
intrinsic angular momentum.
From
Quantum Physics by Zettili (easily my favorite textbook on the subject, dense and complete):
In the Stern-Gerlach experiment, a beam of silver atoms passes through an inhomogeneous (nonuniform) magnetic field...we would expect classically to see on the screen a continuous band that is symmetric about the undeflected direction...According to Schrodinger's wave theory, however, if the atoms had an orbital angular momentum l, we would expect the beam to split into an odd (discrete) number of 2l+1 components. Experimentally, however, the beam behaves according to the predictions of neither classical physics nor Schrodinger's wave theory. Instead, it splits into two distinct components...
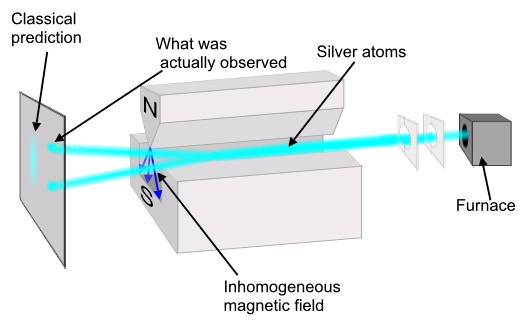 |
| (Sauce: wiki) |
This experimental result
only made sense when one suggests that the particle carries an inherent angular momentum. Not only that, but this spin comes in discrete values. Imagine if you could only spin in your chair at specific speeds (lost in thought, too fast, and nauseating). And then forget that image, because you weren't actually spinning in any spatial direction, you merely
contain "spin". Ridiculous, I know. As Zettili puts it, "The spin, an intrinsic degree of freedom, is a purely quantum mechanical concept with no classical analog".
As stated, spin comes in discrete values; specifically it comes in half-integer values - 0, 1/2, 1, 3/2, 2 (all multiplied by Planck's constant, as so many quantum characteristics are), and so on. Finally we approach the issue brought up at the beginning of this post:
spin is the defining characteristics of bosons and fermions.
Bosons have "integral" spin; 0, 1, 2, etc. This class of particles most importantly contains the photon (and of course, the Higgs).
Fermions have spins like 1/2, 3/2, 5/2, etc, named "half-odd-integral spin" (because even halves like 2/2 is just 1). The most significant fermion is the electron, but also includes protons, neutrons and quarks.
So what's the importance of making this distinction?
 |
| (a) Asymmetric and... |
 |
| (b) ...symmetric wave functions (wiki) |
Without getting into the details, having a half-odd or integer spin defines how you interact with other, identical particles. You can define a group of identical particles by a wave function, and a group of fermions (half-odd spin) has a wave function which is described as
asymmetric (Figure a above), while a group of bosons would be described by a symmetric wave (b above).
In the symmetric case, nothing particularly interesting occurs; you can effectively stuff as many bosons as you want into one space, and the wave function accommodates them quite pleasantly, not unlike being able to add as many musical notes to a chord as you like. The wave abides.
 |
| "That Higgs is really keeping this room together." |
However, in the asymmetric case, the wave function describing the state of multiple identical particles does a funny thing; if you pretend to put two fermions in the same state, the value of the wave function goes to zero. That is, such a wave function doesn't exist,
can't exist, under the constraints of quantum mechanics. This results in the popular
Pauli exclusion principle; try as you like, you simply can't stuff as many electrons as you like into one state: this exclusion repels the electrons away from each other, quite strongly. This "
degeneracy" (multiple particles occupying the same energy level) is responsible for the relative "imperviousness of solid matter" in the case of electrons, and what keeps
neutron stars from collapsing (as fermions, neutrons also are constrained by exclusion).
This principle is also the reason for electrons taking positions of increasing energy states in atoms. In fact, it is at the core of all atomic and chemical interactions. It defines much of the character of the periodic table as well. The rows are made by increasing the number of electrons within a "shell", with each subsequent row representing a larger shell, and each column representing similar "filling" of each shell. In fact, without this exclusion (that is, if electrons were bosons), the universe would be a very dull place indeed, as all the electrons of an atom would fall to the ground state, and all atoms would behave the same.
This all tells you pretty much nothing about the Higgs, but I hope it illuminates just a little bit more of the universe.
 |
| (sauce: chemicool.com) |






